
앞에서 살펴본 곡선 피팅 문제에서는 입력 변수가 하나였지만, 실제 입력 변수의 종류는 매우 다양하다. 이렇게 고차원 입력 변수를 다루는 것은 패턴 인식에서 중요한 고려 사항이다.


해당 문제를 살펴보기 위해 위 데이터를 예시로 들었다. 위 데이터로 하고자 하는 것은 \(x_{6}\)과 \(x_{7}\)이 있을 때, 해당 데이터가 무슨 Label을 가지는지 분류하는 것이다. Label의 종류는 색으로 나타나있다.
위 그림에서 \(\times\) 표시의 데이터가 새로 들어왔을 때, 해당 데이터를 무슨 Label로 분류할 수 있을지 생각해보자. \(\times\) 주위에 빨간색과 초록색이 있고 파란색을 멀리 떨어져있으므로 빨간색 혹은 초록색일 것이다.
이런 방식으로 새로운 데이터를 분류하기 위한 가장 단순한 접근법은 Figure 1.20처럼 입력 공간을 여러 칸으로 나누어 각 칸에 가장 많이 있는 데이터의 Label을 해당 칸에 Label로 설정하여 분류하는 것이다.
하지만 이 단순한 접근법은 입력 변수가 많아져 입력 공간의 차원이 높은 경우에 문제가 발생한다.

(Figure 1.21)
왼쪽의 그림처럼 입력 공간의 차원이 높아짐에 따라 필요한 칸의 수가 기하급수적으로 증가하고 각 칸이 비어 있지 않도록 하기 위해 수많은 훈련 데이터가 필요해진다.
이를 통해 입력 변수의 개수가 많아지면 이런 단순한 접근법을 적용하기 어렵다는 사실이 명확해졌고 더 나은 접근법이 필요하다는 것을 알았다.
고차원 공간에서 발생하는 문제점을 더 살펴보기 위해 다른 예시를 들어볼 것이다. 첫 번째로는 다항식 공선 피팅 문제를 다변수 입력 공간에 적용해보는 것이다.

위 다항식은 \(D\)개의 입력 변수가 있을 경우 3차 계수까지 나타낸 형태이다. \(D\)가 증가함에 따라 계수의 숫자는 \(D^{3}\)에 비례하여 증가하고 3차 다항식이 아닌 \(M\)차 다항식을 사용한다면 \(D^{M}\)에 비례하여 증가한다. 입력 변수의 개수가 증가할수록 거듭 제곱 형태로 계수가 증가하는 것이다.
두 번째로는 고차원에서는 우리가 3차원에서 얻은 직관과는 다른 기하학적인 직관에 대해 알아볼 것이다. 간단한 예로 \(D\)차원의 반지름 \(r=1\)인 구체와 \(r=1-\epsilon\)인 구체 사이에 존재하는 부피의 비율을 계산할 것이다.
\(D\)차원에서 반지름 \(r\)을 가진 부피는 \(r^{D}\)에 비례하고 다음과 같이 나타낼 수 있다.

\(K_{D}\)는 \(D\)에 따른 상수이기 때문에 위에서 언급한 \(r=1\)인 구체의 부피에서 \(r=1\)인 구체와 \(r=1-\epsilon\)인 구체 사이에 존재하는 부피의 비율은 다음과 같이 계산할 수 있다.

위 식의 값을 \(D\)와 \(\epsilon\)에 따라 그래프로 나타내면 다음과 같다.

(Figure 1.22)
\(D=1\)일 때는 1과 \(1-\epsilon\)의 거리이기 때문에 선형이고 \(D=2\)는 원의 넓이에 따른 비율을 나타낸다.
차원이 커질수록 작은 \(\epsilon\)에서 비율이 1에 가까워지며 이는 고차원에서는 구체 부피의 대부분이 표면 근처에 얇은 껍질에 집중되어 있다는 것이다.
이런 현상을 패턴 인식과 직접적으로 연관되어 있는 가우시안 분포에서도 나타난다. 가우시안 분포를 데카르트 좌표에서 극좌표로 변환한 뒤 방향성 변수들을 적분으로 없애면 원점에서부터 반지름 \(r\)에 대한 함수 \(p(r)\)로 나타낼 수 있다.
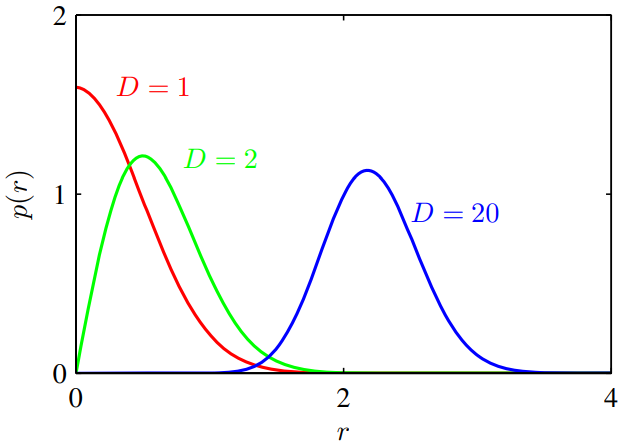
(Figure 1.23)
\(p(r)\delta r\)은 반지름 \(r\)상에 \(\delta r\)의 두꼐에 해당하는 확률 직량을 나타내며 이 분포의 그래프를 \(D\)에 따라 그려놓은 것이 Figure 1.23이다.
해당 예시에서도 \(D\)가 커질수록 가우시안 확률 질량이 얇은 겉껍질에 집중되는 것을 확인할 수 있다.
(가우시안 분포의 극좌표 변환은 차후 해당 글에 작성할 예정입니다.)
이처럼 고차원에서 발생할 수 있는 문제를 차원의 저주(curse of dimensionality)라고 한다. 해당 글에서는 쉬운 이해를 위해 주로 일차원 또는 이차원의 입력 공간을 예시로 들지만, 저차원 공간에서 발전시킨 아이디어가 반드시 고차원에서도 적용되지 않는다는 사실을 염두에 두어야 한다.
그러나 고차원 입력값에 대해 사용할 수 있는 효과적인 패턴 인식 테크닉을 찾아내는 것은 불가능하지 않다.
첫 번째 이유는 실제 타겟 변수에 유의미한 변화를 일으키는 입력 변수의 개수는 제한되어 있기 때문이다.
두 번째 이유는 실제 세계의 데이터는 매끈한 특성(smoothness properties)을 가지고 있기 때문에 입력 값의 작은 변화는 타겟 값에서도 작은 변화만을 일으키고 따라서, 보간법 등의 테크닉을 사용할 수 있기 때문이다.
Reference: Pattern Recognition and Machine Learning
'Machine Learning > PRML' 카테고리의 다른 글
| [PRML] 1.3. Model Selection (0) | 2023.01.02 |
|---|---|
| [PRML] 1.2. Probability Theory (1) | 2022.11.28 |
| [PRML] 1.1. Example: Polynomial Curve Fitting (0) | 2022.11.20 |



댓글