Factor Graph는 확률 분포나 함수를 도식적으로 나타낸 것이다. 이 그래프는 Factor Node(■)와 Variable Node(○)로 구성된 Bipartite Graph이다. Edge에 방향성을 주어 방향성 혹은 비방향성 Graph로 나타낼 수 있으며 그래프의 특징을 활용하여 확률 분포해 Marginalization을 효율적으로 표현할 수 있다.
Factor Graph에 들어가기 앞서 대표적인 Factor 연산으로 Product와 Marginalization이 있다.
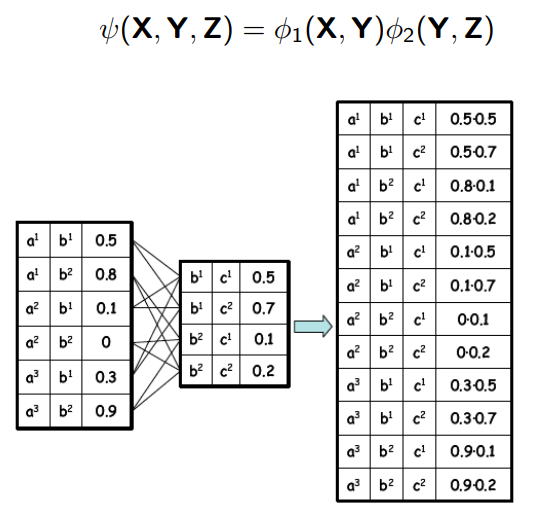

Factor는 Variable이 입력되면 입력에 맞는 Output를 출력하는 함수 혹은 확률 변수를 말한다.
Product는 두 Factor의 Variable들을 한 번에 갖고 두 Factor의 Output 곱을 출력하는 Factor(joint distribution)를 계산하는 연산이고 Marginalization은 Product와 반대로 하나의 Variable을 입력으로 하지 않을 때의 Output을 계산하는 연산이다.

위와 같이 5개의 변수를 갖는 PDF(Probability Density Fuction)가 있고 이는 4개의 Factor로 표현될 수 있다. 이를 Factor Graph로 표현한다면 아래와 같다.

\(v, w, x, y, z\) 다섯 개의 변수를 Variable Node로 사이에 Factor Node를 두었다. Factor Node는 입력 받는 Variable과 연결되어 있다. PDF를 Factor Graph로 나타내었을 때, 어떤 이점이 있는지 예를 들어 설명해본다.
만약 위 PDF에서 \(p(w)\)를 구하고 싶다면 아래과 같이 \(f_{1}(v,w)f_{2}(w,x)f_{3}(x,y)f_{4}(x,z)\)를 w에 대해 sum out(\(w\)를 제외한 모든 변수에 대해 Summation)하면 된다(Marginalization).

\(v,x,y,z\)가 각각 K개의 값을 가지고 있다면 위 연산은 \(O(3K^{4})\)의 곱셈 연산과 \(O(K^{4}\)의 덧셈 연산을 필요로 한다. 하지만 우리가 \(ca+cb\)를 할 때, \(c(a+b)\)를 하면 연산이 줄어들 듯, Factor Graph를 사용한다면 보다 쉽게 Margianalization 연산량을 줄일 수 있다.

\(p(w)\)는 위와 같이 Summation에서 공유하는 Variable이 없다면 두 합의 곱으로 묶을 수 있다. 그리고 이 분리는 Factor Graph에서 보다 쉽게 표현할 수 있다.

이렇게 \(w\)를 기준으로 나뉘는 두 부분을 Factor Graph에선 Message로 정의한다. \(m_{f_{1}\to w}(w)\)는 Factor \(f_{1}\)에서 Variable \(w\)로 가는 Messgae를 나타내고 \(m_{f_{2}\to w}(w)\)는 Factor \(f_{2}\)에서 Variable \(w\)로 가는 Messgae를 나타낸다.

최종적으로 \(p(w)\)를 구하기 위해 모든 연산을 Message 단위로 분리하면 위와 같다. 위 식에서 확인할 수 있듯이 Message에는 Factor에서 Variable로 가는 Message가 있고, Variable에서 Factor로 가는 Message도 있다.
Factor에서 Variable로 가는 Message는 해당 Factor로 오는 이전의 Message에 해당 Factor를 곱한다. 예를 들어 \(m_{f_{2}\to w}(w)\)는 \(x\)에서 \(f_{2}\)로 가는 Message인 \(m_{x\to f_{2}}(w)\)에 \(f_{2}(w,x\)를 곱하고 해당 식를 \(w\)에 대해 sum out하여 계산한다. 물론 \(p(w)\)를 구하기 위한 연산이므로 \(w\)에서 \(f_{2}\)로 가는 Message인 \(m_{w\to f_{2}}(w)\)는 연산에 포함시키지 않는다.
Variable에서 Factor로 가는 Message는 해당 Varible로 향하는 모든 Message를 곱한다. 예를 들어 \(m_{x\to f_{2}}(x)\)는 \(x\)로 향하는 두 Factor \(f_{3}\)과 \(f_{4}\)의 Message인 \(m_{f_{3}\to x}(x)\)과 \(m_{f_{4}\to x}(x)\)의 곱으로 계산한다. 마찬가지로 \(p(w)\)를 구하는 과정이므로 연산의 반대 방향인 \(f_{2}\)에서 \(x\)로 향하는 Message인 \(m_{f_{2}\to x}(x)\)는 곱하지 않는다.
이를 수식으로 표현하면 아래와 같다.

: Marginal Probability인 \(p(t)\)는 \(t\)과 근접한 Factor에서 오는 Message의 곱을 통해 계산할 수 있다.

: Factor \(f\)에서 \(t_{1}\)으로 가는 Message는 \(t_{1}\)을 제외하고 \(f\)로 가는 모든 Message와 \(f\)의 곱을 \(t_{1}\)에 대해 sum out하여 계산할 수 있다.
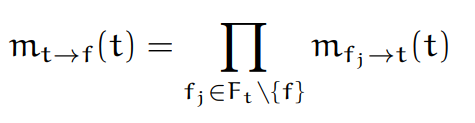
: \(t\)에서 Factor \(f\)로 가는 Message는 \(f\)를 제외하고 \(t\)와 근접한 모든 Factor Node로부터 오는 Message의 곱으로 계산할 수 있다.
Lecture References
https://www.cs.toronto.edu/~urtasun/courses/GraphicalModels/lecture4.pdf
https://www.cs.toronto.edu/~urtasun/courses/GraphicalModels/lecture7.pdf
'Machine Learning' 카테고리의 다른 글
| Bayesian Inference (0) | 2022.11.01 |
|---|

댓글